Mathematics Formulas Demystified Quadratics, Trig, Derivatives, Integrals & More

Mathematics Formulas Demystified Quadratics, Trig, Derivatives, Integrals & More
Mathematics Formulas Demystified: Quadratics, Trig, Derivatives, Integrals & More 1. Cross Multiplication
Explanation: Cross multiplication is a fundamental technique used in solving equations involving fractions. It’s particularly useful in solving proportions and linear equations with fractional coefficients.
2. Quadratic Equations
Explanation: Quadratic equations are second-degree polynomial equations. Your page can cover topics such as the quadratic formula, factoring, completing the square, and graphing quadratic functions.
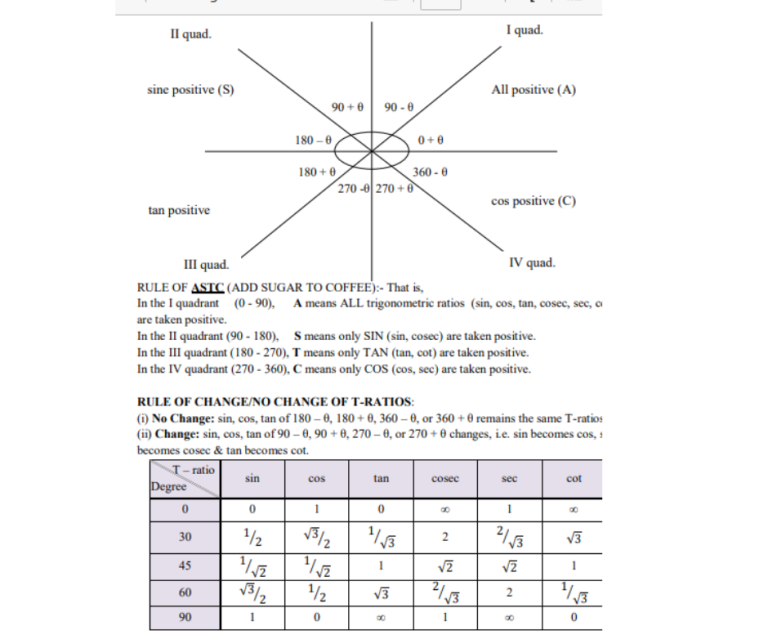
3. Trigonometry
Explanation: Trigonometry deals with the study of angles and the relationships between the sides and angles of triangles. You can cover trigonometric functions (sine, cosine, tangent, etc.), the unit circle, and trigonometric identities.
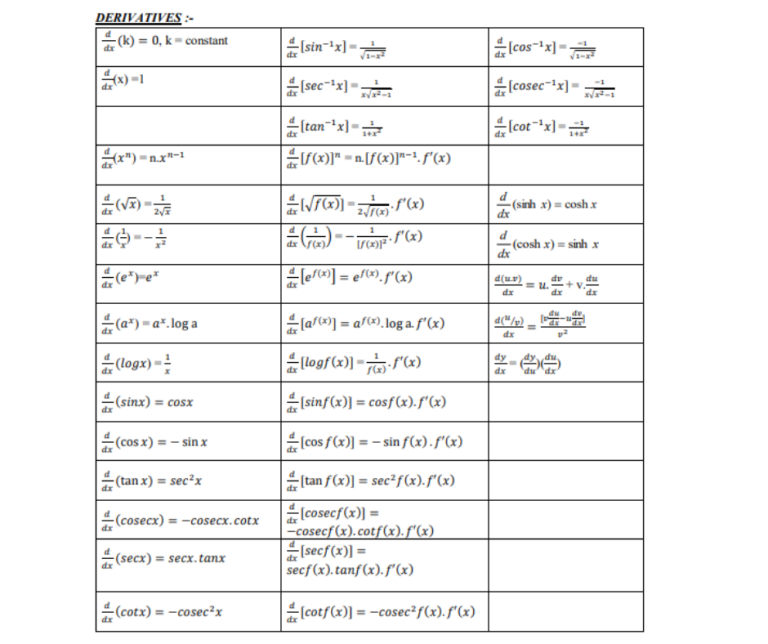
4. Derivatives
Explanation: Derivatives are a crucial concept in calculus. Explain how to find derivatives of functions using rules like the power rule, chain rule, and product rule. Include applications in rates of change and optimization.
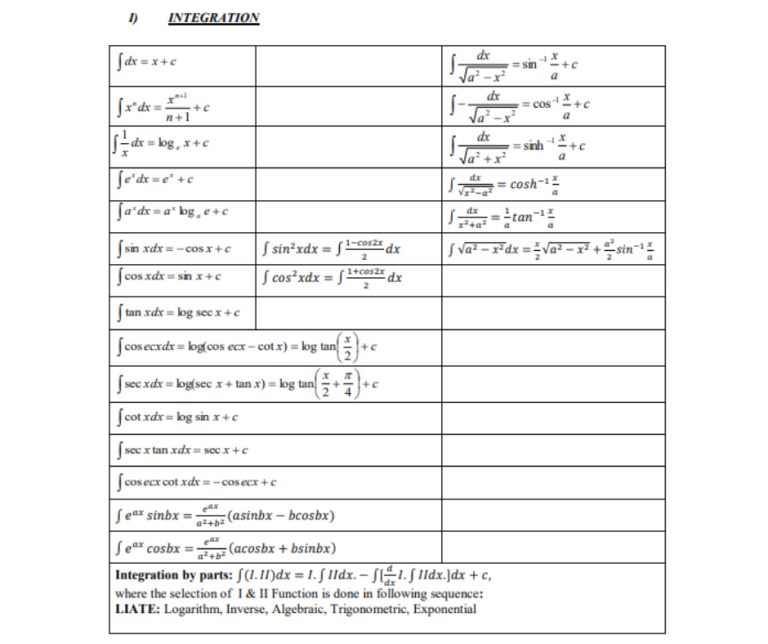
5. Integration
Explanation: Integration is the reverse of differentiation and is used to find the area under curves. Discuss techniques like integration by parts, substitution, and definite vs. indefinite integrals.
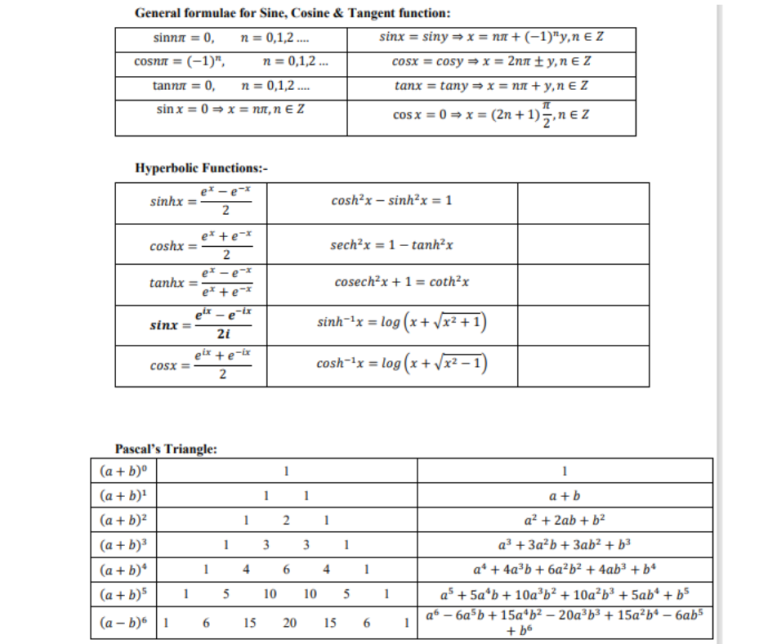
6. Hyperbolic Functions
Explanation: Hyperbolic functions are analogs of trigonometric functions for hyperbolas. Include definitions, properties, and applications in calculus and physics.
7. Pascal’s Triangle
Explanation: Pascal’s Triangle is a mathematical array with various applications in combinatorics and probability. Explain its construction and how it’s used in binomial expansion and probability calculations.
8. Partial Fractions
Explanation: This topic deals with breaking down complex fractions into simpler ones. Explain the process of partial fraction decomposition, including linear and irreducible quadratic factors.
9. Logarithms
Explanation: Logarithms are used to solve equations involving exponents. Cover the properties of logarithms, logarithmic rules, and applications in exponential growth and decay.
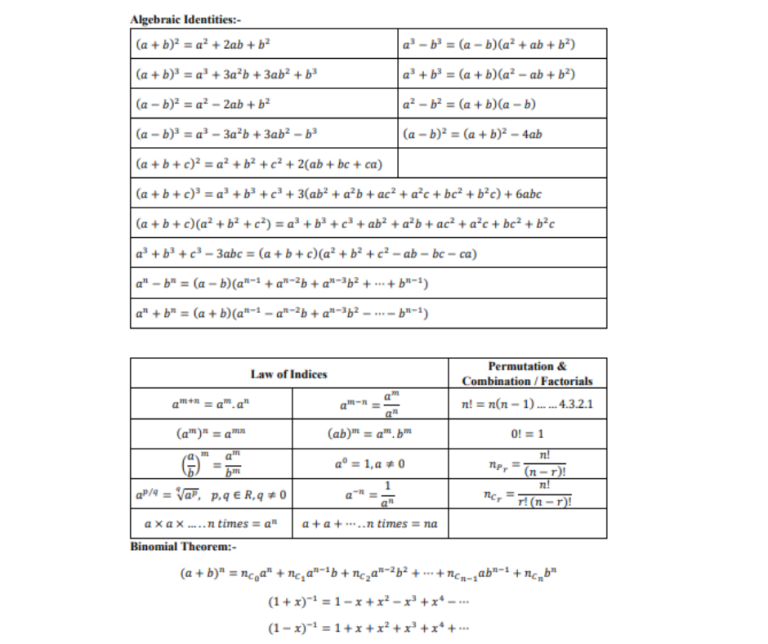
10. Algebraic Identities
– Explanation: Algebraic identities are equations that hold true for all values of the variables involved. Include common identities like the distributive property and the Pythagorean identity.
11. Binomial Theorem
– Explanation: The binomial theorem is used to expand expressions of the form (a + b)^n. Explain the formula, coefficients, and applications in probability and algebra.
Mathematics Formulas Demystified Quadratics, Trig, Derivatives, Integrals & More

Mathematics Formulas Demystified Quadratics, Trig, Derivatives, Integrals & More

Mathematics Formulas Demystified Quadratics, Trig, Derivatives, Integrals & More

Mathematics Formulas Demystified Quadratics, Trig, Derivatives, Integrals & More


FAQ for Mathematics Formulas Demystified: Quadratics, Trig, Derivatives, Integrals & More
Q1: What is cross multiplication, and when is it used? A1: Cross multiplication is a technique for solving equations with fractions. It’s used when you need to find a missing value in a proportion or solve linear equations with fractional coefficients.
Q2: What are quadratic equations, and what topics can I explore related to them? A2: Quadratic equations are second-degree polynomial equations. You can explore topics like the quadratic formula, factoring, completing the square, and graphing quadratic functions.
Q3: What does trigonometry involve, and what are some key concepts to cover? A3: Trigonometry deals with angles and relationships in triangles. Key concepts include trigonometric functions (sine, cosine, tangent), the unit circle, and trigonometric identities.
Q4: Why are derivatives important, and what can I learn about them? A4: Derivatives are crucial in calculus for understanding rates of change and optimization. You can learn how to find derivatives using rules like the power rule, chain rule, and product rule.
Q5: What is integration, and what techniques can I explore in this topic? A5: Integration is the reverse of differentiation and is used to find the area under curves. Techniques include integration by parts, substitution, and understanding definite vs. indefinite integrals.
Q6: What are hyperbolic functions, and where are they applied? A6: Hyperbolic functions are analogs of trigonometric functions for hyperbolas. They have applications in calculus and physics due to their unique properties.
Q7: How does Pascal’s Triangle work, and where is it used? A7: Pascal’s Triangle is a mathematical array with applications in combinatorics and probability. It’s used in binomial expansion and probability calculations.
Q8: What is partial fraction decomposition, and when is it used? A8: Partial fractions break down complex fractions into simpler ones. Learn the process, including handling linear and irreducible quadratic factors.
Q9: How do logarithms work, and where are they applied? A9: Logarithms are used to solve exponential equations. Explore logarithmic properties, rules, and applications in exponential growth and decay.
Q10: What are algebraic identities, and why are they important? A10: Algebraic identities are equations that hold true for all values of the variables involved. They are essential for simplifying expressions and solving equations.
Q11: What is the binomial theorem, and what can I learn about it? A11: The binomial theorem is used to expand expressions like (a + b)^n. Understand the formula, coefficients, and applications in probability and algebra.